`hbonds` command¶

The hbonds command detects and reports hydrogen bonds in molecules. The hbonds command has the following features:

It identifies hydrogen bonds between backbones, sidechains, subunits and ligands.
It has a flexible interface to identify a wide-range of hydrogen bond types including amide, aliphatic, hydroxyl and the specification of arbritrary electric dipole types.
It classifies backbone-backbone hydrogen bonds based on backbone torsion angles.
Helical stretches require contiguous residues with helical backbone torsion angles. This prevents the misclassification of 310-helices and beta turns as well as isolated i+3, i+4 and i+5 hydrogen bonds.

$  ml hbonds --help
usage: mollib hbonds [-h] -i id/filename [id/filename ...] [-c filename] [-l]
                     [-s] [-m [MODELS [MODELS ...]]] [--hydrogenate]
                     [--aliphatic] [--detailed] [--sort-type]

arguments:
  -h, --help            show this help message and exit
  -i id/filename [id/filename ...], --in id/filename [id/filename ...]
                        (required) The filename(s) or PDB identifier(s) of the
                        structure(s)
  -c filename, --config filename
                        The configuration filename
  -l                    List details on the molecule(s)
  -s, --save            Save fetched files to the local directory.
  -m [MODELS [MODELS ...]], --models [MODELS [MODELS ...]]
                        The models numbers to analyze.
  --hydrogenate         Strip hydrogens and re-add them before analysis

hbond options:
  --aliphatic           Includes aliphatic hydrogen bonds
  --detailed            Report detailed information on hydrogen bonds.
  --sort-type           Sort hydrogen bonds by type

Note

If the molecule does not have hydrogens, this command will need to be run with the --hydrogenate parameter. See the hydrogenate option.

Arguments¶

--aliphatic: (Optional) Include aliphatic hydrogen bonds in the results. The acceptor-donor atom cutoff distances are elongated to 3.0 A, and carbon atoms are allowed in hydrogen bond donor dipoles.
--detailed: (Optional) Present a detailed report on the geometries of hydrogen bonds. The detailed table does not include classification information.
--sort-type: (Optional) Sort the hydrogen bonds by classification type, like beta-sheet or alpha-helix.

Examples¶

In this example, the hemagglutinin fusion peptide structure (-i 2KXA) is downloaded, and its amide hydrogen bonds are reported.

$  ml hbonds -i 2KXA
Table: Hydrogen bond listing for 2KXA-1

Num  Donor       Acceptor    Classification                    E (kT) / Prob.  
---- ----------- ----------- --------------------------------- ----------------
1    A.G1.H1--N  A.G20.O--C  bb-bb amide (isolated)            1.4 / 23.6%     
2    A.G1.H2--N  A.W21.O--C  bb-bb amide (isolated)            3.5 /  3.1%     
3    A.A5.H--N   A.G1.O--C   bb-bb amide (isolated)            1.2 / 31.4%     
4    A.I6.H--N   A.L2.O--C   bb-bb amide (alpha-helix/N-term)  3.0 /  4.8%     
5    A.A7.H--N   A.F3.O--C   bb-bb amide (alpha-helix/N-term)  7.5 /  0.1%     
6    A.G8.H--N   A.G4.O--C   bb-bb amide (alpha-helix)         6.2 /  0.2%     
7    A.F9.H--N   A.A5.O--C   bb-bb amide (alpha-helix)         0.7 / 51.7%     
8    A.I10.H--N  A.I6.O--C   bb-bb amide (alpha-helix)         1.2 / 31.5%     
9    A.E11.H--N  A.A7.O--C   bb-bb amide (alpha-helix/C-term)  3.0 /  4.8%     
10   A.G12.H--N  A.G8.O--C   bb-bb amide (alpha-helix/C-term)  5.6 /  0.4%     
11   A.G13.H--N  A.F9.O--C   bb-bb amide (isolated)            3.2 /  4.0%     
12   A.G16.H--N  A.G12.O--C  bb-bb amide (isolated)            4.6 /  1.0%     
13   A.M17.H--N  A.G13.O--C  bb-bb amide (isolated)            0.0 / 100.0%    
14   A.M17.H--N  A.W14.O--C  bb-bb amide (310-helix)           4.4 /  1.2%     
15   A.I18.H--N  A.W14.O--C  bb-bb amide (alpha-helix/N-term)  8.9 /  0.0%     
16   A.D19.H--N  A.T15.O--C  bb-bb amide (alpha-helix/N-term)  2.0 / 13.8%     
17   A.G20.H--N  A.G16.O--C  bb-bb amide (alpha-helix)         0.0 / 100.0%    
18   A.W21.H--N  A.M17.O--C  bb-bb amide (alpha-helix/C-term)  0.4 / 68.9%     
19   A.Y22.H--N  A.I18.O--C  bb-bb amide (alpha-helix/C-term)  3.6 /  2.7%     
20   A.G23.H--N  A.D19.O--C  bb-bb amide (isolated)            1.2 / 31.1%     
21   A.S24.H--N  A.Y22.O--C  bb-bb amide (isolated)            5.0 /  0.7%

This example downloads a crystal structure of ubiquitin (-i 1UBQ), adds hydrogens to the structure and shows part (|head -n15) of its amide hydrogen bond report.

$  ml hbonds -i 1UBQ --hydrogenate|head -n15
Table: Hydrogen bond listing for 1UBQ

Num  Donor            Acceptor       Classification                    E (kT) / Prob.  
---- ---------------- -------------- --------------------------------- ----------------
1    A.M1.H2--N       A.V17.O--C     bb-bb amide (isolated)            6.2 /  0.2%     
2    A.I3.H--N        A.L15.O--C     bb-bb amide (sheet)               2.0 / 13.8%     
3    A.F4.H--N        A.S65.O--C     bb-bb amide (sheet)               1.3 / 27.3%     
4    A.V5.H--N        A.I13.O--C     bb-bb amide (sheet)               0.2 / 81.8%     
5    A.K6.H--N        A.L67.O--C     bb-bb amide (sheet)               1.2 / 30.0%     
6    A.T7.H--N        A.K11.O--C     bb-bb amide (sheet)               2.9 /  5.6%     
7    A.T9.H--N        A.T7.OG1--CB   bb-sc amide (isolated)            1.0 / 36.3%     
8    A.G10.H--N       A.T7.O--C      bb-bb amide (type I turn)         3.3 /  3.7%     
9    A.I13.H--N       A.V5.O--C      bb-bb amide (sheet)               2.8 /  5.8%     
10   A.L15.H--N       A.I3.O--C      bb-bb amide (sheet)               2.1 / 12.4%     
11   A.V17.H--N       A.M1.O--C      bb-bb amide (isolated)            1.8 / 16.7%

Theory¶

Hydrogen bonds are defined between a donor dipole, which includes a hydrogen atom, and an acceptor dipole. The acceptor and donor dipoles are more than simple electric dipoles. The electric dipole-dipole energy is minimized when the two dipoles are aligned colinearly (head-to-toe) with respect to each other. Hydrogen bonds involve the sharing of a hydrogen atom between a donor atom (N) and an acceptor atom (O) and the distribution of electron density between these atoms and the hydrogen atom. Consequently, hydrogen bonds are arranged according to the molecular orbitals between the donor and acceptor atoms, rather than simply the electric potential between atoms. As a result, optimal hydrogen bonds are askew from a standard electric dipole.

Geometry¶

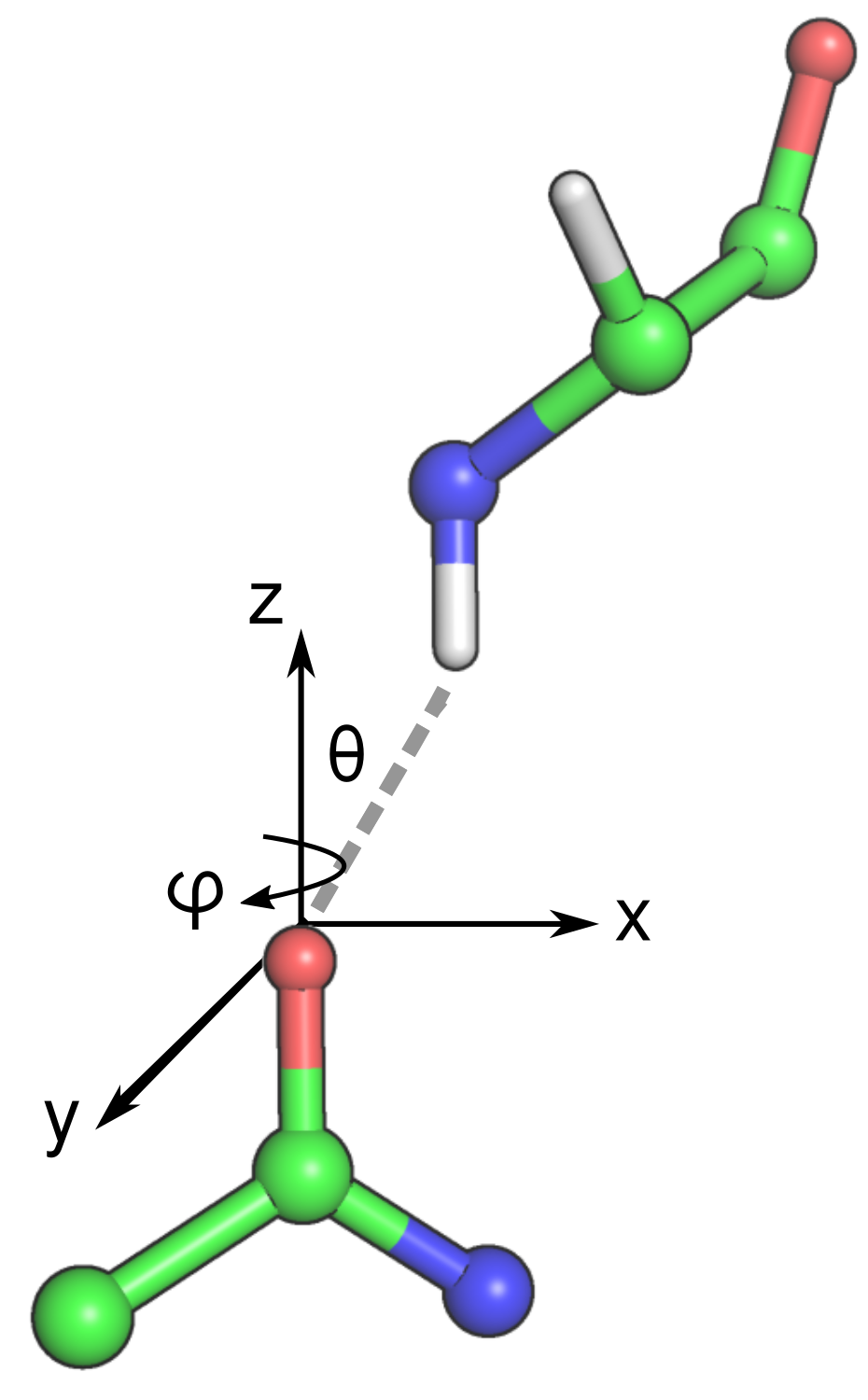
A hydrogen bond has an acceptor dipole and a donor dipole. The donor dipole has a d1 donor atom (H) and a d2 donor atom (N, O or C), and the acceptor has an a1 acceptor atom (O) and an a2 acceptor atom (C). The geometry of a hydrogen bond is defined by the distance of the d1a1 vector (\(d_{d1a1}\)), the \(\theta\) angle and the \(\phi\) angle.

The geometry of a hydrogen bond.

\(d_{d1a1}\) distance (in Angstroms): The distance between the d1 donor atom (H) and the a1 acceptor atom (O).
\(\theta\) angle (in degrees): The angle between the d1a1 vector and the z-axis of the acceptor dipole. The z-axis of the acceptor dipole is defined by the normalized vector formed between the acceptor a1 and a2 atoms.
\(\phi\) angle (in degrees): The angle between the d1a1 vector and the x-axis of the acceptor dipole plane. The acceptor dipole plane is defined by the the acceptor dipole atoms and the next heaviest atom bound to atom a2.

Energy and Probabilities¶

The reported probabilities are determined from a histogram of the \(d_{d1a1}\) distance, the \(\theta\) angle and the \(\phi\) angle compared to a set of ca. 11,300 high-resolution crystal structures in the PDB. A high probability indicates that the measured hydrogen bond geometries are observed frequently in high-resolution structures. Conversely, a low probability indicates that a particular hydrogen bond geometry is rarely seen in high-resolution structures. These are typically colored in yellow (relatively rare) or red (very rare).

The energies represent a potential of mean force (PMF) calculated from a Boltzmann inversion.

\[E(\Omega) = -kT ln[P(\Omega)]\]

The energy (in units of kT) is calculated from the Boltzmann constant and temperature (\(kT\)) and the probability of finding the specific configuration, \(\Omega\). The configuration, in this case, is defined by the \(d_{d1a1}\) distance, the \(\theta\) angle and the \(\phi\) angle. The energy is 0 for an ideal hydrogen bond, and it increases as the hydrogen bond deviates from ideality–according to the probability of finding a specific geometry in high-resolution structures.

hbonds command¶